Energy cluster formation
For almost 20 years now, it has been an established, experimentally verified fact that in the vibrational states of the H2Se molecule, at high J and Ka values the rotational energies form four-member groups of nearly degenerate levels, so-called energy clusters. Realistic quantum mechanical calculations have shown that the H2S, H2Te and H2Po molecules exhibit similar effects. In the 1990s we were concerned with the theoretical description of the energy clusters of triatomic molecules, mostly by variational calculations, i.e., calculations of the rotation-vibration energies by diagonalization of a matrix representation of the rotation-vibration Hamiltonian. The four-fold clusters were initially predicted by classical and semi-classical theory, and we have shown how these predictions are borne out by experiment and by quantum mechanical calculations. Analysis of rotation-vibration wavefunctions obtained from variational calculations provides a simple picture of the rotational motion in the cluster states: The molecule rotates around one of its two bonds in a clockwise or an anticlockwise manner. The two choices for the bond, and the two choices for the sense of the rotation provide a total of four equivalent situations corresponding to a four-fold energy cluster.
The following diagram illustrates the four equivalent situations that give rise to a fourfold cluster state in a triatomic molecule.
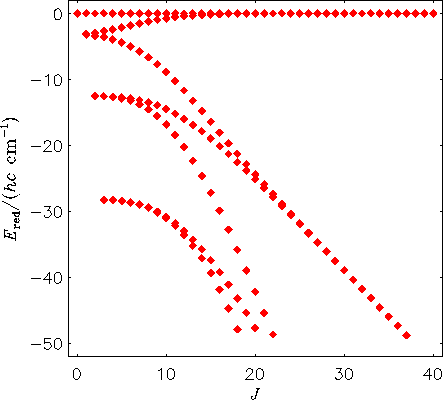
The energy level structure of a rigidly rotating H2130Te molecule. The term values are plotted relative to the highest term value for each J multiplet.
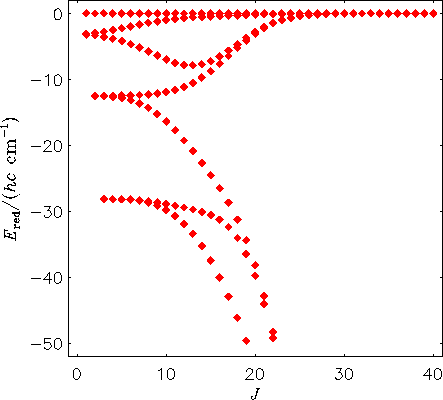
The next diagram shows the rotational energy level structure in the vibrational ground state of the H2130Te molecule, calculated directly from the potential energy function of the molecule with the MORBID program. The term values are plotted relative to the highest term value for each J multiplet. The calculated spacings are in good agreement with values derived from experiment.
Comparison of the two figures shows that when we allow the molecule to vibrate, its rotational energy structure changes drastically at high J: four-fold energy clusters form.
At the beginning of the 21st century, the existence of energy clusters in triatomic molecules had been experimentally verified and the clusters had been analyzed in quantum mechanical, variational calculations. It was also well known that in spherical top molecules such as CH4 and CF4, energy clusters are formed. Hence, it seemed likely that in symmetric top molecules of type XH3, which are "in between" the asymmetric tops H2X and the spherical tops XH4, energy clusters would form. However, for the XH3 molecules, there had been no investigations, neither experimental nor theoretical, of energy cluster formation.
In collaboration with Dr. Sergei N. Yurchenko, Technical University Dresden, Germany, and Prof. Walter Thiel, Max Planck Institute for Coal Research, Mülheim/Ruhr, Germany, we developed the program XY3 for the variational calculation of the rotation-vibration energies of a pyramidal XH3 molecule in an isolated electronic state. We subsequently used this program to investigate theoretically a possible energy cluster formation at high rotational excitation in phosphine PH3.
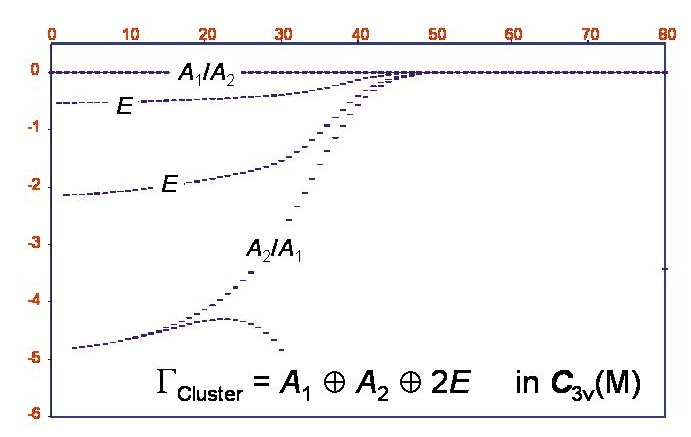
Rotational term values in the vibrational ground state of the phosphine molecule.
The XY3 calculations indeed showed that in the vibrational ground state of PH3, six-fold energy clusters are formed at high rotational excitation. The figure shows a term value diagram for the vibrational ground state of PH3; the abscissa = J and the ordinate is the term value in cm-1, relative to the highest term value at the given J-value. The cluster state has a total degeneracy of six and has the symmetry A1+A2+2E in the molecular symmetry group C3v(M).
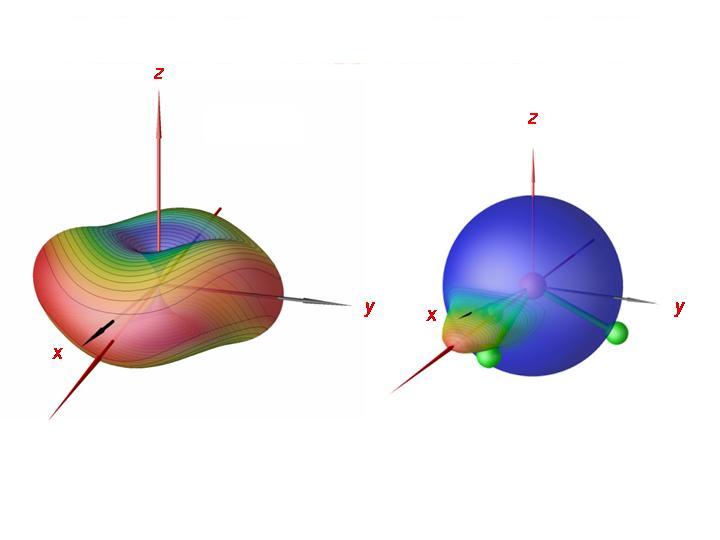
By analyzing the rotation-vibration-wavefunctions obtained in the XY3 calculations, we could show that in the cluster states, the PH3 molecule rotates about one of it bonds, clockwise or anticlockwise. There are now three bonds and two possibilities for the sense of the rotation. This gives rise to six equivalent situations, corresponding to a six-fold energy cluster. In the right-hand display of the figure, we have imaged, for a cluster state at J = 80, the probability distribution for the direction of the angular momentum vector relative to the molecule onto a sphere. It is seen that the molecule rotates about an axis that nearly coincides with one of its bonds. In the left display, we show the semiclassical rotational energy surface for J = 80. The semiclassical analysis confirms the quantum mechanical results; the molecule rotates about one of its bonds.
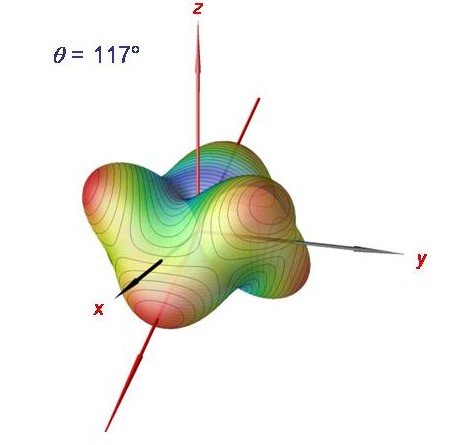
Rotational energy surface for phosphine at J = 120.
The semiclassical analysis in terms of rotational energy surfaces can be carried out for very large J-values. We show here the rotational energy surface for J = 120. It has six equivalent maxima, each one corresponding to one of the six degenerate cluster states.
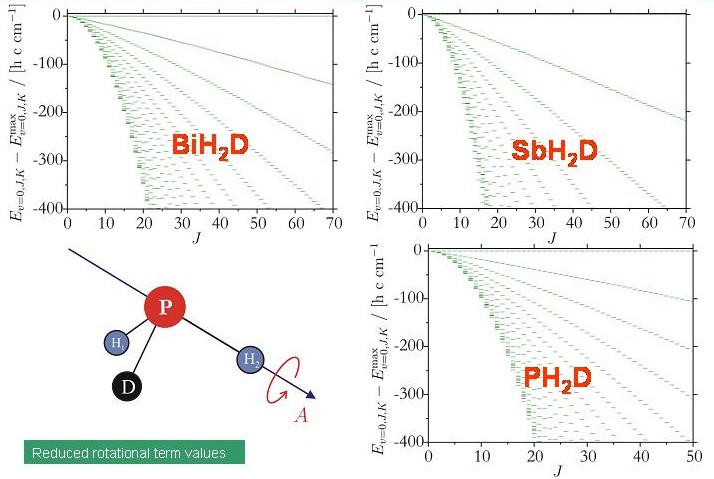
After the completion of the program system TROVE (Theoretical ROtation-Vibration Energies, developed in collaboration with Dr. Sergei N. Yurchenko, Technical University Dresden, Germany, and Prof. Walter Thiel, Max Planck Institute for Coal Research, Mülheim/Ruhr, Germany) we are able to calculate variationally the rotation-vibration energies of an arbitrary molecule in an isolated electronic state. We used the new program to investigate theoretically the energy cluster formation in the deuterated molecules XH2D and XHD2 (X = Bi, Sb, P). The diagram shows term value diagrams for the XH2D molecules considered. There are no discernable energy clusters.
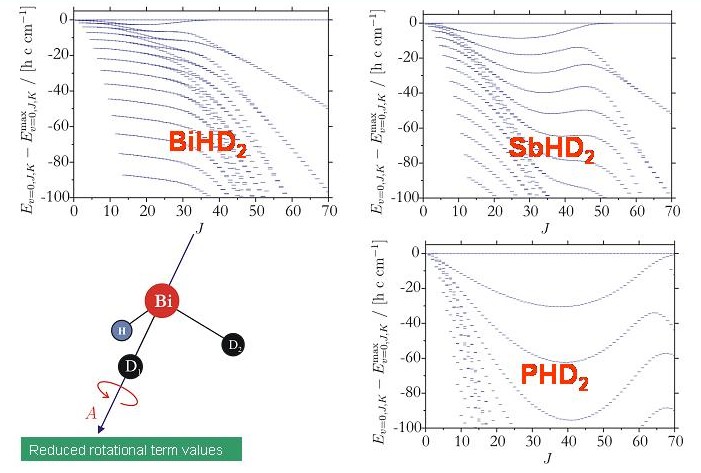
By contrast, the rotation-vibration energies of the XHD2 molecules exhibit four-fold clusters easily recognizable in the term value diagrams of these molecules. The energy cluster formation in the XHD2 molecules is highly analogous to that of H2X molecules (see above).
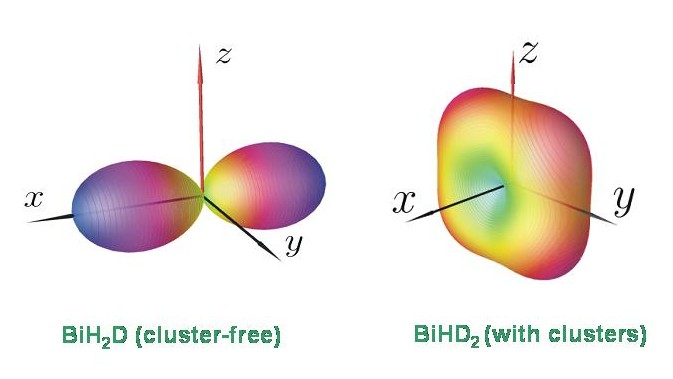
At present it is unclear why, for example, BiHD2 exhibits four-fold energy cluster formation while BiH2D does not. However, the energy level patterns calculated with TROVE are in keeping with the results of a semiclassical analysis in terms of rotational energy surfaces. The diagram shows the rotational energy surfaces for BiH2D and BiHD2 at J = 80. The rotational energy surface for BiHD2 has four equivalent maxima, corresponding to a four-fold cluster. The rotational energy surface for BiH2D has two equivalent maxima only, and so this molecule has only the doubly degenerate clusters expected for a rigid asymmetric top.
Publications on energy clusters
S. N. Yurchenko, R. I. Ovsyannikov, W. Thiel, and Per Jensen: Rotation-Vibration Energy Cluster Formation in XH2D and XHD2 Molecules (X = Bi, P, and Sb), J. Mol. Spectrosc. 256, 119-127 (2009).
S. N. Yurchenko, W. Thiel, and Per Jensen: Rotational energy cluster formation in XY3 molecules: Excited vibrational states of BiH3 and SbH3, J. Mol. Spectrosc. 240, 197-210 (2006).
S. N. Yurchenko, W. Thiel, Per Jensen, and P. R. Bunker: Rotation-vibration energy level clustering in the X2B1 ground electronic state of PH2, J. Mol. Spectrosc. 239, 160-173 (2006).
S. N. Yurchenko, W. Thiel, S. Patchkovskii, and Per Jensen: Theoretical Evidence for the Formation of Rotational Energy Level Clusters in the Vibrational Ground State of PH3, Phys. Chem. Chem. Phys. 7, 573-582 (2005).
P. R. Bunker and Per Jensen: Chirality in Rotational Energy Level Clusters, J. Mol. Spectrosc. 228, 640-644 (2004).
Per Jensen: An Introduction to the Theory of Local Mode Vibrations, Mol. Phys. 98, 1253-1285 (2000). Article prepared by invitation.
Per Jensen, G. Osmann, and I. N. Kozin: The Formation of Four-fold Rovibrational Energy Clusters in H2S, H2Se, and H2Te, in: "Advanced Series in Physical Chemistry", vol. 9, "Vibration-Rotational Spectroscopy and Molecular Dynamics" (D. Papousek, Ed., ISBN 981-02-1635-1), pp. 298-351, World Scientific Publishing Company, Singapore, 1997.
P. C. Gomez, L. F. Pacios, and Per Jensen: Fourfold Clusters of Rovibrational Energies in H2Po Studied with an ab initio Potential Energy Function, J. Mol. Spectrosc. 186, 99 (1997).
P. C. Gomez and Per Jensen: A Potential Energy Surface for the Electronic Ground State of H2Te Derived from Experiment, J. Mol. Spectrosc. 185, 282 (1997).
